Assignment -
Question 1. Let (T, ∧, ∨,', 0, 1) be a Boolean Algebra.
Define ∗ : T × T → T and o : T × T → T as follows:
x ∗ y := (x ∨ y)' x o y := (x ∧ y)'
(a) Show, using the laws of Boolean Algebra, how to define x ∗ y using only x, y, o and parentheses.
(b) Show, using the laws of Boolean Algebra, how to define x o y using only x, y, ∗ and parentheses.
Define R ⊆ T × T as follows: (x, y) ∈ R if, and only if, (x ∧ y) ∨ (x' ∧ y') = 1
(c) Show, using the laws of Boolean Algebra, that R is an equivalence relation. Hint: You may want to use the observation that if A = B = 1 then A ∧ B ∧ C = A ∧ B implies C = 1 (why?)
Question 2. Let P F denote the set of well-formed propositional formulas made up of propositional variables, T, ⊥, and the connectives ¬, ∧, and ∨. Recall from Quiz 7 the definitions of dual and flip as functions from PF to PF:
|
|
|
|
|
|
|
|
|
- dual(φ ∧ ψ) = dual(φ) ∨ dual(ψ)
|
- flip(φ ∧ ψ) = flip(φ) ∧ flip(ψ)
|
- dual(φ ∨ ψ) = dual(φ) ∧ dual(ψ)
|
- flip(φ ∨ ψ) = flip(φ) ∨ flip(ψ)
|
(a) For the formula φ = p ∨ (q ∧ ¬r):
(i) What is dual(φ)?
(ii) What is flip(φ)?
(b) Prove that for all φ ∈ PF: flip(φ) is logically equivalent to ¬dual(φ).
Question 3. Let P(n) be the proposition that: for all k, with 1 ≤ k ≤ n,
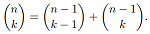
(a) Prove that P(n) holds for all n ≥ 1. (Note: it is possible to do this without using induction)
We can compute 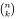 from the formula given in lectures, however this can often require computing unnecessarily large numbers. For example,
from the formula given in lectures, however this can often require computing unnecessarily large numbers. For example,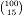 = 253338471349988640 which can be expressed as a 64-bit integer, but 100! is larger than a 512-bit integer. We can, however, make use of the equation above to compute
= 253338471349988640 which can be expressed as a 64-bit integer, but 100! is larger than a 512-bit integer. We can, however, make use of the equation above to compute 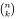 more efficiently. Here are two algorithms for doing this:
more efficiently. Here are two algorithms for doing this:

Let trec(n, k) be the running time for chooseRec(n, k), and let titer(n) be the running time for chooseIter(n, k). Let Trec(n) = max0≤k≤n trec(n, k) and Titer(n) = max0≤k≤n titer(n, k) (so Trec(n) ≥ trec(n, k) for all k, and likewise for Titer(n)).
(b) Give an asymptotic upper bound for Trec(n). Justify your answer.
(c) Give an asymptotic upper bound for Titer(n). Justify your answer.