problem 1: A large book publisher has five manuscripts which must be edited as soon as possible. Five editors are accessible for doing the work; though their working times on the different manuscripts will vary based on their backgrounds and interests. The publisher wants to use an assignment method to find out who does what manuscript. Each editor will edit only one manuscript. Estimates of editing times (in hrs) for each and every manuscript by each editor are:
                           Editor
Manuscript    A      B     C     D      E

1                 12    8     10    16    14
2                  9    10    14    13    10
3                 17    14    9     18    8
4                 15    7     11     9    17
5                 12    18    22    11   25

a) Formulate the problem as an assignment model, show all the decision variables and constraints.

b) Determine the total minimum editing time?  What editors will be assigned to each and every manuscript?

problem 2: A thief breaks into a house. He searches and finds numerous items of value. He carries with him a sack that can hold 8 cubic feet of items and he can carry 100 pounds of stolen goods in his sack. He predicts that if he is in the house longer than four minutes he will get caught, he wants to leave before this occurs? The given table contains information regarding each of the items he can acquire.

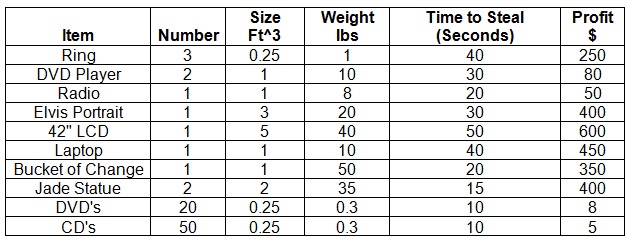
a) Formulate the problem as an integer programming problem. State the complete model comprising all the decision variables and constraints.

b) Specify what items and how many of each the thief must steal.

c) Determine the limiting constraint(s), the size of the sack, the weight he can carry or the amount of time that he has.

d) What is his gain for this endeavor?

problem 3: A city is reviewing the position of its fire stations. The city is made up of a number of neighborhoods, as shown in figure below. A fire station can be positioned in any neighborhood. This is capable to handle the fires for both its neighborhood and any adjacent neighborhood. The objective is to minimize the number of fire stations employed.

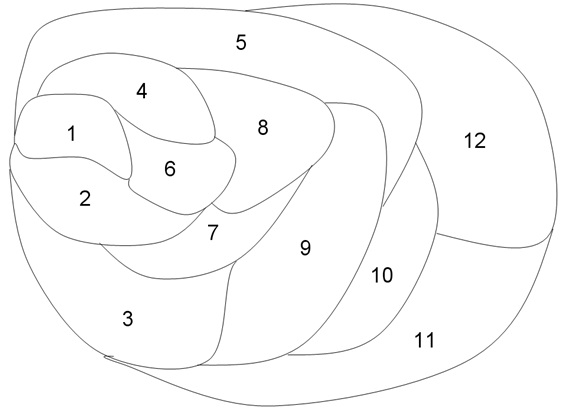
i) Formulate the problem as a binary-integer programming problem. State the complete model comprising all the decision variables and constraints.

ii) State what neighborhoods must contain a fire station.

iii) In addition to part B, provide two more feasible solutions to this problem. Which solution is best, justify.