problem 1: Answer in short:

a) List out the rotational symmetry axes in a face centered orthorhombic crystal system.

b) Draw the first Brillouin zone for a 2-D oblique reciprocal lattice.

c) Why are X-rays with energies ∼ few keV needed to probe crystal structures by diffraction methods?

d) describe the bonding method in hydrogen fluoride (HF).

e) Compute the group velocity and phase velocity of a longitudinal wave propagating all along a linear monoatomic chain, if its frequency is ω = √K/M where m is the mass of the atom and K is the force constant.

f) What is the importance of Debye frequency?

g) Compute the fraction of electrons excited above the Fermi level in Al at room temperature, given that the Fermi energy of Al is 11.1 eV.

h) Describe why the resistivity of a semiconductor reduces with increasing temperature.

i) Differentiate between Type I and Type II superconductors.

j) What are the uses of photo-conducting materials?

problem 2:

a) The primitive translation vectors of the hexagonal space lattice are given by:

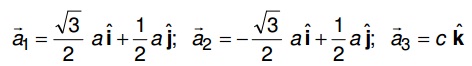
Find out the volume of the primitive cell and the reciprocal lattice vectors.

b) Obtain the structure factor for Na and CsCl both of which form a bcc lattice.

c) List out the symmetries of the CH₃OH molecule.

d) Find out the radius of the largest sphere that can be fitted in the centre of a mono atomic fcc unit cell.

problem 3:

a) Compute the equilibrium lattice energy per mole of NaCl that has a lattice constant a = 5.63 Å, n = 8.4 and a Madelung constant of 1.748. (Take ε₀ = 8.85 × 10⁻¹² Farad m⁻¹.)

b) Compute the heat capacity of Hf at 200 K, given that its Debye temperature is 242 K.

c) The interatomic spacing of a 1D lattice of atoms of mass 5.0 × 10⁻²⁷ kg is 4.0 Å. The force constant is 2.0 × 10⁻² Nm⁻¹.

Compute the maximum frequency that can be supported by this lattice.

d) The longitudinal and transverse velocities in nickel all along the [100] direction are 5.30 km s⁻¹ and 3.65 km s⁻¹, correspondingly. The transverse velocity in the [110] direction is 2.26 km s⁻¹. The density of nickel is 8.90 g cm⁻³. Compute all the independent elastic stiffness constants.

problem 4:

a) Compute the Fermi energy of a monovalent bcc solid whose lattice constant is 5.1Å.

b) Find out the energy and momentum of an electron at the boundary of the first Brillouin zone of a square lattice with a side of 3.0 Å.

c) Find out the change in the Femi level of GaAs as the temperature changes from 0 K to 300 K. The band gap E_g =1.42 eV and the effective mass of the electron and hole are 0.068 me and 0.56 me correspondingly.

d) Compute the superconducting transition temperature of a substance for which the critical fields at 14 K and 13 K are 1.4 × 10⁵ T and 4.2 × 10⁵ T correspondingly.

problem 5:

a) Compute the molar diamagnetic susceptibility for Li in its ground (1s) state.

b) describe the technique used to grow crystals of the compound semiconductor GaAs.

c) describe the various kinds of polymerization processes with an illustration of each.

d) Describe the properties of thin film materials and their subsequent applications.