Mathematics- Algebraic Geometry Problem

Let K denotes an algebraically closed field and let P¹ be constructed as in Example 5.5(a) in Gathmanns notes, i.e. P¹ is the gluing of X₁ = A¹ and X₂ = A¹ along  the open subsets U12 = A¹\{0} ⊆ X₁ and U₂₁ = A¹\{0} ⊆ X₂, where U12 and U21 is identified by the isomorphism

U₁₂ → U₂₁,

t ι→ t^-1

We let i₁ : X₁ → P₁ and i₂ : X₂ → P¹ denote the associated morphisms.

1) Show that the map

π : A2\{0} → P¹

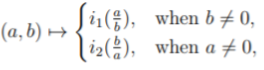
is well defined and surjective.

For elements (a, b), (c, d) ∈ A²\{0} we write  (a, b) ∼ (c, d) when (a, b) and (c, d) are linearly dependent as elements in the K-vector space K².

2) Show that ∼ defines an equivalence relation on A²\{0}.

3) Show that π induces a bijective map

π^- = (A²\{0})/∼ → P¹

[(a, b)] ι→ π(a, b).

Attachment:- Assignment File.rar