Problem 1: Review the concept of fluxes

What are the mass flow rates through each of the surfaces described below and shown in the figure? For some of these cases, you are free to justify your answer with words, rather than mathematics.

a) A circular surface area A with unit normal nˆ = 1/√2(eˆ₁ + eˆ₂).
b) A circular surface of area A with unit normal nˆ = eˆ₂.
c) A circular surface of area A with unit normal nˆ = eˆ₁.
d) A hemisphere whose cross-sectional area is A with unit normal nˆ = eˆ₁.
e) A sphere whose cross-sectional area is A, that is, its radius is √A/Π.

Problem #2: Volumetric flow rates

Given the fluid velocity profile, calculate the volumetric flow rate through the tube for the following cases. (Hint: Don't forget the ‘r'-weighting when you integrate over the cross section of the cylindrical tube.)

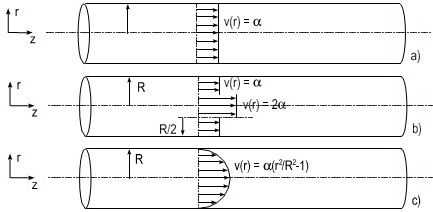
a) A plug flow where the fluid has a velocity of v(r) = α at all points.

b) A flow with v(r) = α for r ≥ R/2 and v(r) = 2α for 0 ≤ r < R/2. 2 2

c) Now try a continous velocity field: a Poiseuille flow, where v(r) = α(r /R -1).

Problem #3: Work Problem 2-6 in the textbook.

Problem #4: Work Problem 3-10 from the textbook.

Problem #5: Evaluation of thermal conductivity

To determine the thermal conductivity of a new plastic, the plastic has been rolled into a tube with an inner diameter of 4 inches and a thickness of 0.252 inches. The plastic was found to conduct 3.0 watts for every foot of pipe length at steady state when temperature probes attached to the inside and outside of the pipe indicated respective wall temperatures of 26^oC and 24^oC.

a) Derive an explicit expression for the thermal conductivity k in terms of the energy transfer per length of pipe Q_l, inner and outer radius (r_i and r_o), and temperatures (T_i and T_o).

b) Substitute the appropriate values to determine the thermal conductivity of the plastic in units of cal sec^-1 cm^-1 K^-1?

c) What assumptions have you made in order to determine the conductivity?